Cards In This Set
| Front | Back |
|
Period of a graph
|
When equation: y=asin(bx+c)+dNote: the fuction could be sine,cos,tan,csc,sec, and cotsine and cosine: 2pi/b--> and csc and sectangent: pi/b--> and cot
|
|
Phase Shift formula of a graph
|
For all equations: y=asin(orcos,tan...)(bx+c)+dPhase shift= -c/b
|
|
Sine graphs
|
Some things to remember: - the zero's of a sin graph will always be: (pi/b,a) and (2pi/b, a) and (0,0) -->This is WITHOUT the PHASE SHIFT!!!!- A regular sin graph has a period of 2pi. Steps(for complex graph)in : y=asin(bx+c)+d1. determine the period using 2pi/b2. Using this value create 4 points on the x-axis3. Graph y=asinbx4.Determine the phase shift: -c/b and shift your graph5. Then move it d vertically. If d is positive, move it up, if negative, down. *You can use the zero values as help.*For absolute value's: just remember that everything will be above the x-axisFor negative graphs, remember everything will be flipped
|
|
Cosine Graphs
|
Some thing helpful to remember:The zero's for a cosine graph are (3pi/2b, a) and (pi/ 2b, a). This is WITHOUT PHASE SHIFTS!!!!- A regular cosine graph has a period of 2pi
Steps (for complex graphs):in: y=acos(bx+c)+d1. determine period: 2pi/b2. Divide period by 4 and label the 4 points on x-axis3.Using these points, graph y=acosbx4. Determine phase shift (-c/b) and shift graph5. Using d move it vertically, same principles as sin apply*Use zero values to help you* |
|
Tangent Graphs
|
 Zeros for tangent (WITHOUT PHASE SHIFT):(-pi/4b, -a) and (pi/4b, a).for y=atan(bx+c)+d1. determine period2. determine ASYMPTOTES: do this for y=atanbx:values where y is undefined are the asymptotesRemember, if there is no phase shift, the graph will intersect (0,0). 3. Graph you zero's. 4. Apply phase shift and vertical shift Here it is vital to use zeros, they are very helpful |
|
Graphing csc graphs
|
The best way to graph a csc graph is to graph the sin graph of the same equation first. Then, the zeroes of this sine graph will be the asymtotes of the csc graph. Using the "Vertices" make a "U". Refer to Graphing sin funcions flashcard.
|
|
Graphing sec graphs
|
The best way to graph a sec graph is to graph the cos graph of the same equation first. Then, the zeroes of this cosine graph will be the asymtotes of the sec graph. Using the "Vertices" make a "U". Refer to Graphing cosine funcions flashcard.
|
|
Graphing cot graphs
|
Zeroes:(pi/4b, a) and (3pi/4b, -a) WITHOUT phase shifts
Similar steps as tan, only graph is in other direction. Refer to tanx flashcard. Just remember cot x is 1/tanx |
|
Pythagorean identities |
  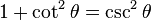 |



