Cards In This Set
| Front | Back |
|
9.1.1 State the independence of the vertical and the horizontal components
of velocity for a projectile in a uniform field
|
² Projectile: body moving in
free motion
² Free motion has gravity and
air resistance
n Air resistance/friction:
negligible
n Gravity: downward force
² Horizontal velocity: 0 (no force)
² Vertical velocity: accelerating downward (gravity)
² Result in parabola
|
|
9.1.2 Describe and sketch the trajectory of projectile motion as parabolic
in the absence of air resistance.
|
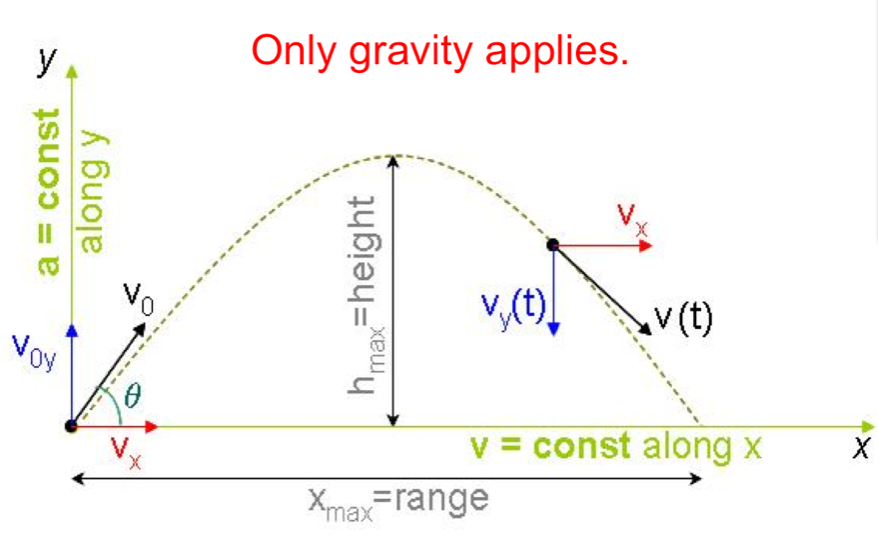 Refer to image |
|
9.1.3 Describe qualitatively the effect of air resistance on the trajectory
of a projectile.
|
²
Shorter range
²
Lower height
Why?
Air resistance against the velocity of the trajectory
|
|
9.2.1 Define gravitational potential and gravitational potential energy
|
Gravitational
Potential:
² Work done per unit mass to bring a point mass from
infinity to that point
Gravitational Potential
Energy:
² Energy needed to perform gravitational potential
Gravitational Constant:
6.67 * 10-11 Nm2kg-2
|
|
9.2.2 State and apply the expression for gravitational potential due to a
point mass
|
 Refer to image |
|
9.2.3 State and apply the formula relating gravitational field strength to gravitational
potential gradient
|
Gravitational Field
Strength (I)= - ΔV / Δx
|
|
9.2.4 Determine the potential due to one or more point masses
|
 V = -G {(M1 / x) + (M2 / r-x)} |
|
9.2.5 Describe and sketch the pattern of equipotential surfaces due to one
and two point masses
|
 Refer to image |
|
9.2.6 State the relation between equipotential surfaces and gravitational
field lines
|
Gravitational lines ⊥ equipotential surface
|
|
9.2.7 Explain the concept of escape speed from a planet
|
² The minimum initial speed at surface of a body
required to escape a body’s gravitational field.
² M IS BEG:
Minimum Initial Speed for Body to
Escape Gravitational field
|
|
9.2.8 Derive an expression for the escape speed of an object from the
surface of a planet
|
|KE| = |PE|
|0.5mvescape2| = |-GMem/Re|
vescape = √2GM/R
vescape on earth = √2g0Re
( g0 = GMe / Re2) |
|
9.3.1 Define electric potential and electric potential energy
|
 Electrical potential at a point in a field: ² Work done per unit charge in bringing a positive test charge from infinity to the point in the field. V = ,k∗point charge-distance from point charge. ² Electrical potential energy of a point charge at any point: Work done in moving the charge from infinity to that point |
|
9.3.2 State and apply the expression for electric potential due to a point
charge
|
 Refer to image |
|
9.3.3 State and apply the formula relating electric field strength to
electric potential gradient
|
Potential gradient:
Work done to move a charge from one potential to another
= qΔV W = FΔx FΔx = qΔV = −,△V-△x. |
|
9.3.4 Determine the potential due to one or more point charges
|
 Refer to image |



