Cards In This Set
| Front | Back |
|
11.1.1 - Describe the
nature of standing (stationary waves)
|
A standing
wave is the product of the propagation of 1 wave against a wall and its
reflected wave with the same speed, same wavelength, same amplitude, opposite
direction.
Because the wave is
reflected, the energy that is propagated returns to the same point of origin.
Velocity=displacement / time, and since there is no displacement, the wave has
no velocity. As well, we say that no energy is propagated
|
|
11.1.2 - Explain the
formation of one-dimensional standing waves
|
As one wave
is propagated at a certain fundamental frequency by the vibration of a source
and at point B, it hits point A and is reflected back to point B at 𝜋 out of phase (i.e. as
a particle on the forward wave reaches its amplitude, a particle in the same
position on the reflected wave is half way to its amplitude) forming a standing
wave with a greater amplitude
|
|
11.1.3 - Discuss the modes
of vibration of strings and air in open and in closed pipes
|
 Refer to image |
|
11.1.4 - Compare standing
waves and travelling waves
|
 Refer to image |
|
11.2.1 - Describe what is
meant by the Doppler effect
|
This effect is the change in
the frequency of a wave received by an observer, compared to the frequency with
which it was emitted. The effect takes place whenever there is motion
between the emitter and receiver
|
|
11.2.2 - Explain the Doppler
effect by the reference to wavefront diagrams for moving-detector and
moving-source
|
The source moves towards observer B and
away from observer A. The wavecrests are piling in front of the source and thus
the crests reach B at time intervals which are shorter than those on emission.
|
|
11.2.3 - Apply the Doppler effect
equations for sound
|
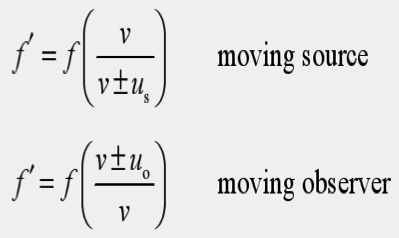 Refer to image |
|
11.2.6 - Outline an example in
which the Doppler effect is used to measure speed
|
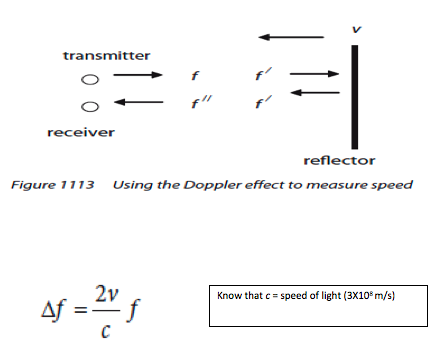 Refer to image |
|
11.3.1 - Sketch the
variation with angle of diffraction of the relative intensity of light
diffracted at a single slit
|
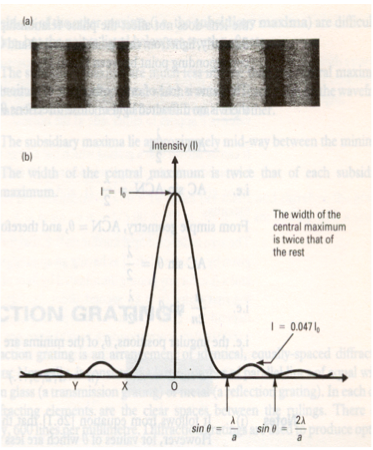 Refer to image |
|
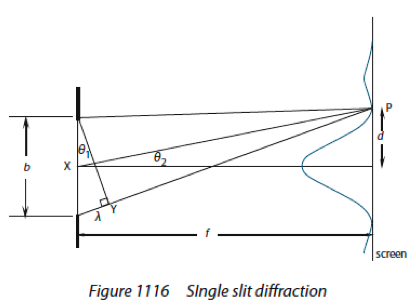
Derive the formula Ѳ=λ/b. for the position
of the first minimum of the diffraction pattern produced at a single slit
|
 Refer to image Note that both angles are very small, hence equated to Ѳ. This equation gives half the angular width of the central maximum |
|
11.4.1 - Sketch the variation with
angle of diffraction of the relative intensity of light emitted by two point
sources that has been diffracted at a single slit
|
 Refer to image |
|
11.4.2 - State the Rayleigh
criterion for images of two sources to be just resolved
|
CMOFM – Central Maximum over First Minimum
If the central maximum of one diffraction
pattern coincides with the first minima of the other diffraction pattern then
the two sources will just be resolved
|
|
11.4.3 - Describe the significance of resolution in the development of devices
such as CDs and DVDs, the electron microscope and radio telescopes
|
Radio
Telescopes – the wavelength of radio waves is large, so the telescope needs to
be large so that the resolution is good
CDs – the
information on the drive is read by lasers reflecting from the surface. A laser
with a higher resolution can read more information from the surface of a disk.
Electron
Microscope – electrons are propagated with a very short wavelength through a
species. Hence, the image produced is very clear due to the microscope’s high
resolution power
|
|
11.5.1 - Describe what is meant by
Polarized light
|
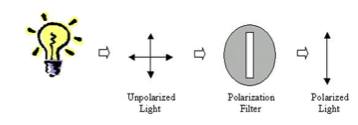 Light consists of vibrations in every direction. If the vibrations are only allowed in one direction, light is polarized |
|
11.5.2 - Describe polarization by
reflection
|
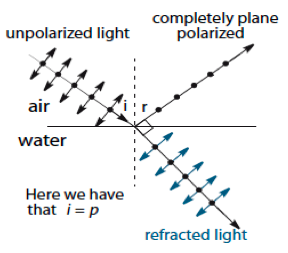 When unpolarized light falls on a material the reflected light is usually partially polarized. At one particular angle, called the polarization angle, the partially reflected light is completely polarized. At this angle the partially reflected ray and the refracted ray are at right angles to each other. The vibrations in the partially reflected ray are parallel to the surface. |



