Cards In This Set
| Front | Back |
|
KinematicsUnits and Dimensionsc = centi = 10-xm = mili = 10-xµ = micro = 10 -xn = nano = 10-xp = pico= 10-xG/B = giga = 10xM = mega = 10xk = kilo = 10x
|
-2-3-6-9-12963
|
|
KinematicsKinematicsKinematics is the description of motion in terms of an object's position, velocity, and acceleration.
Displacement (Δx) is the change in _____;It is a ____ quantity. Displacement does not depend on the path between the initial and final points. The average velocity is also a vector quantity and takes the same direction as Δx. Velocity tells us how fast an object's position. V = Δx/Δt Velocity changes if the speed or direction changes. Average Speed = total distance traveled divided by the time = d/Δt and is a scalar quantity and has no direction. |
Position; vector
|
|
KinematicsKinematicsVelocity tells us how fast and object's position changes; acceleration tells us how fast an object's _____ changes. *If velocity is changing, then there is acceleration. If acceleration points in the same direction as the initial velocity, then the object's speed is _____. If the acceleration points in the direction opposite to the initial velocity, then the object's speed is _____.
acceleration = Δv/Δt |
Velocity
increasing decreasing |
|
KinematicsUniformly Accelerated MotionIn uniformly accelerated motion, acceleration is constant. v =v0 + at
Δx = 1/2(v0 + v)t Δx = v0t + 1/2at2 Δx = vt - 1/2at2 v2 = v02 +2ad + 1/2at2 In free fall, weight = gravity and acceleration = 9.8 m/s |
Review
|
|
KinematicsKinematics with GraphsWhen plotting Δx vs. Δt, the slope is the ____. And when plotting Δv vs. Δ t, the slope is the ____. The area under a velocity vs. time graph gives the displacement.
Free FallIn free fall there is constant acceleration. g = acceleration due to gravity |
Velocity
acceleration |
 KinematicsProjectile MotionAn object experiencing only the constant, downward acceleration due to gravity (free fall) is called projectile motion and the path will be a ____. Unlike linear motion, in projectile motion velocity and position components are in both the vertical and horizontal directions thus must be analyzed separately. Horizontal MotionDisplacement: x = V0xtVelocity: vx =v0 (constant)Acceleration: ax = 0 V0x = V Cosθ Vertical MotionDisplacement: y = v0t + 1/2 (-g)t2Velocity: vy = v0y + (-g)tAcceleration: ay = -g V0y = V sinθ tan θ = Ry/ Rxtan-1 (y/x) = θ *If the horizontal acceleration is zero throughout the projectile's flight motion then the horizontal velocity will be constant throughout the flight*If the horizontal velocity does not change then whatever it was initially is all it will ever be. |
Parabola
|
|
KinematicsKinematicsWhen solving a problem with vectors going in different directions, break each down into their x and y components.
Ex: ↖ A =8N ↗B = 4N ↘ C= 8 N θ= 30° Ax = -8 cos 30 Bx = 4 cos 30 Cx = 8 cos 30Ay = - 8 sin 30 By = 4 sin 30 Cy = -8 sin 30 To find the resultant add all components of Rx and Ry. The magnitude of the resultant = √Rx2 + Ry2 |
Review
|
|
MCAT MATHLaws of Exponentsbp x bq =
bp / bq = (bp)q = b0 = b-p = (ab)p = (a/b)p = |
Bp+q
bp-q bpq 1 1/bp apbp ap/bp |
|
MCAT MATHLaws of Radicals√ab =
√a/b = p√ap = |
√a x √b
√a / √b ap/q |
|
MCAT MATHThe X-Plane, Y-Plane and other GraphsLines ~KinematicsThe equation of a line is: y = mx + b m = slope b = y-intercept
|
 Review |
|
MCAT MATHThe X-Plane, Y-Plane and other GraphsParabolas y = kx2 The general form of the equation of a parabola is
a (x-h)2 +k The parabola opens upward if a is ____; if it opens downward if a is ____. The vertical line of symmetry passes through the ____.
|
 Review positive negativevertex |
|
MCAT MATHThe X-Plane, Y-Plane and other GraphsParabolasThe exponential decay curve has the following equation:
y = Ae-kx It intersects the y-axis at (0, A) and as x increases, y decreases. |
 Review |
|
MCAT MATHThe X-Plane, Y-Plane and other GraphsParabolasThe hyperbola graph has the following equation:y = k/x
It is the graph of inverse proportions: for small values of x, the values of y are large and vice versa. |
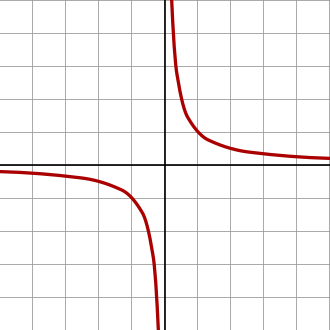 Review |
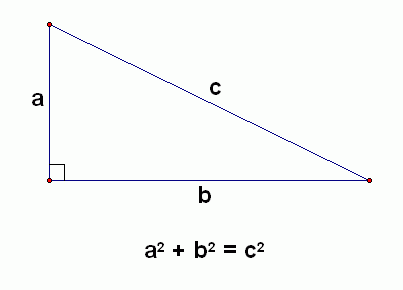 MCAT MATHTrigonometry: Pythagorean Theorem The pythagorean triple is referred to as the 3, 4, 5 triangle. Any multiple of this triangle is considered a pythagorean triple. Sin θ= opp/hypcos θ= adj/ hyptan θ= opp/ adj |
Review
|
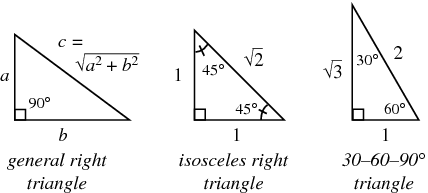 MCAT MATHTrigonometry: Right TrianglesFor an isosceles Right Triangle (2 congruent sides) Both sides are equal to x and hypotenuse = x√2 sin 45 = 1/√2 cos 45 = 1/√2 tan 45 = 1 For a 30-60-90 triangle: short leg= x; long leg = x√3; hypotenuse = 2x sin 30 = 1/2 sin 60 = √3/ 2 cos 30 = √3/ 2 cos 60 = 1/2 tan 30 = 1√3 or √3 /3 tan 60 = √3 |
Review
|



