IB SL PHYSICS 11 TOPIC4

1. mass on spring (eg. bungeejumping) 2. pendulum(eg. swing) 3. object bobbing in water (eg. buoy,boat) 4. vibrating cantilever (eg.diving board) 5. earthquake 6. bouncing ball 7. musical instruments (eg. strings, percussion, brass, woodwinds, vocal chords) 8. heartbeat

Mean Position (Equilibrium Position) –position of object at rest Displacement (x, meters) –distance in a particular direction of a particle from its mean position Amplitude(A or x0, meters) –maximum displacement from the mean position Period (T, seconds) – time taken for one complete oscillation Frequency(f, Hertz) –number of oscillations that take place per unit time Phase Difference –difference in phase between the particles of two oscillating systems

Simple Harmonic Motion (SHM) –motion that takes place when the acceleration of an object is proportional to its displacement from its equilibrium position and is always directed toward its equilibrium position

Kinetic Energy The kinetic energy is a maximum when the bob is travelling fastest; this is at the bottom of the swing. At the top of the swing, the bob is stationary, so the KE is zero. Potential Energy The potential energy is a minimum when the bob is at its lowest point; we take this to be zero. At the top of the swing, the potential energy is a maximum value. Total EnergyIf no energy is lost then the total energy is a constant value. When the bob is swinging, the energy continually changes between kinetic and potential.

Damping: a dissipative force acts on a system in the opposite direction of motion of the oscillating particle
Effect of damping: system loses energy and amplitude

Light damping (under-damping): small resistive force so only a small percentage of energy is removed each cycle - period is not affected - can take many cycles for oscillations to die out (eg: car shock absorbers)
Critical damping : intermediate resistive force so time taken for object to return to mean position is minimum - minimal or no "overshoot" (eg: electric meters with pointers, automatic door closers)
Heavy damping (over damping): large resistive force - can completely prevent any oscillations from taking place - takes a long time for object to return to mean position (eg. oscillations ini viscous fluid)

Natural frequency of vibration: when a system is displaced from equilibrium and allowed to oscillate freely, it will do so at its natural frequency of vibration
Forced oscillations : a system may be forced to oscillate at any given frequency by an outside driving force that is applied to it

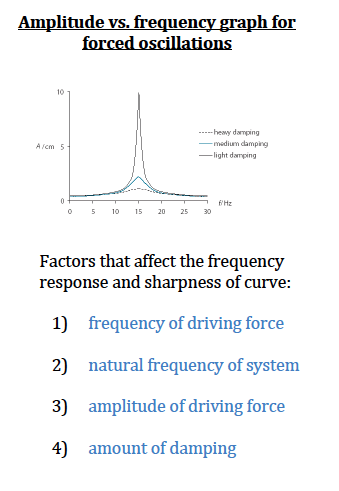See picture

Resonance: a transfer of energy in which a system is subject to an oscillating force that matches the natural frequency of the system resulting in a large amplitude of vibration

Useful resonance-electricity, turning a radio : the natural frequency of the radio circuit is made equal to the incoming electromagnetic wave the electrons will oscillate with the incoming electromagnetic wave. this is turned into sound, through a speaker
-microwave ovens : microwaves are produced at the same frequency as the natural frequency of water molecules water molecules absorb the energy from the microwaves and transfer their energy to the food in the form of thermal energy
Harmful resonance-driving force at resonance increases the oscillations, sometimes this is unwanted-bridges can be destroyed as the wind (driving force) is at the same as the natural frequency. The bridge vibrated and shook itself apart-tower blocks, the same effect as the bridge the wind, or earthquakes, can cause vibrations to destroy the building

Pulse - single oscillation or disturbance
continuous traveling wave - succession of oscillations (series of periodic pulses)
both pulse and traveling waves : there is a transfer energy though there is no net motion of the medium through which the wave passes

Progressive (traveling) waves transfer energy.

A transverse wave : is one in which the direction of the oscillation of the particles of the medium is perpendicular to the direction of travel of the wave ( the energy).
Examples: light, violin and guitar strings, ropes, earthquake S waves
A longitudinal wave : is one in which the direction of the oscillation of the particles of the medium is parallel to the direction of the oscillation of the particles of the medium is parallel to the direction of travel of the wave (the energy).
Examples: sound, earthquake P waves

Wavefront : line (or arc) joining neighboring points that have the same phase or displacement
Ray : line indicating direction of wave motion (direction of energy transfer). Rays are perpendicular to wave fronts.

Crest : points at maximum height of the waveThrough : points at the lowest part of the waveCompression : region where particles of medium are close togetherRarefaction : region where particles of medium are far apart