IB Physics HL Topic 13

The phenomenon where electrons are emitted from the surface of a metal after being exposed to light of a particular frequency called the threshold frequency. Light below the threshold frequency will not cause electrons to be emitted. Above the threshold frequency, the maximum KE of the electrons depends on the frequency of the incident light. The number of electrons emitted depends on the intensity of light, and not the frequency. Emission of electrons is instantaneous, and considers that light can act as particles called photons.

Students should be able to explain why the wave model of light is unable to account for the photoelectric effect, and be able to describe and explain the Einstein model.
Light travels in discrete, packets of energy called photons. The energy of the photon is given by the equation E=hf, where h is Planck’s constant and f is the frequency of the light. The photon explains the photoelectric effect because it shows that light can act as particle and not just a continuous wave of energy. If light traveled solely as a wave, any frequency of light would cause an emission of electrons. This is not the case. The threshold frequency exists, below which no electrons are emitted. E_photon = E_electron + E_kinetic hf =φ+E_k
hf = hf0 + E_k E_k(max) =hf −φ

Millikan’s experiment involving the application of a stopping potential would be suitable.
The Stopping Potential Experiment is used to answer this objective. A simple circuit consisting of an evacuated chamber, voltmeter, ammeter, 
and variable voltage supply was used to determine the maximum KE of the emitted electrons for various frequencies of light. The evacuated chamber consisted of two electrodes (anode and cathode or positive and negative conductors). One electrode
was exposed to incident light. If the light was above the threshold frequency for the
metal electrode, a current registered in the ammeter. The voltage was reversed so
that the electrons causing the current would be repelled. The voltage that reduced
the current to zero, also called the stopping voltage can be used to calculate the
maximum KE of the emitted electrons, Regardless of the intensity of the
light incident on the metal (which increases the current), the stopping voltage is
always the same for a given frequency. E =hf −φ Vsq=hf −φ

Students should also be aware of wave–particle duality (the dual nature of both radiation and matter).
The de Broglie hypothesis states that all particles can act and travel as waves and have an associated wavelength defined λ=p/h, where p is the momentum of the particle, and h is Planck’s constant. Matter waves are the waves associated with particles or matter. They have an associated de Broglie wavelength.

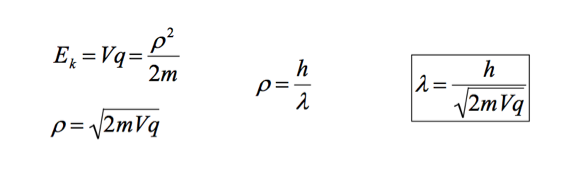A brief outline of the Davisson–Germer experiment will suffice.
One of the experiments used to verify the de Broglie Hypothesis was the Davisson and Germer electron diffraction experiment (not necessary to know name). Davisson and Germer used an electron diffraction pattern to determine the wavelength of an electron. The experimental wavelength corresponded to de Broglie’s calculated wavelength. The wavelength of an electron can be calculated using the de Broglie hypothesis and accelerating an election through a potential difference. The KE of the electron is equivalent to Vq. (KE = Vq).

Students should be able to outline procedures for both emission and absorption spectra. Details of the spectrometer are not required. Emission Spectra — Atomic spectra can be observed by exposing an atom of an element to a continuous source of energy. Examples of laboratory procedures used to produce and observe atomic spectra include the “flame” test and exposing spectral tubes to high voltage Absorption Spectra — View light shining through a sample (usually a gas) with a spectroscope.

An explanation in terms of energy differences between allowed electron energy states is sufficient. Max Planck suggested that electrons change their energy in quantized amounts (E=hf). Spectral lines show that electrons shift orbits releasing or absorbing discrete amounts of energy. Electrons occupy discrete energy levels. Movement between levels involves absorbing or emitting energy. When an electron moves from a higher energy level to a lower energy level, it emits energy in the form of light (photons).

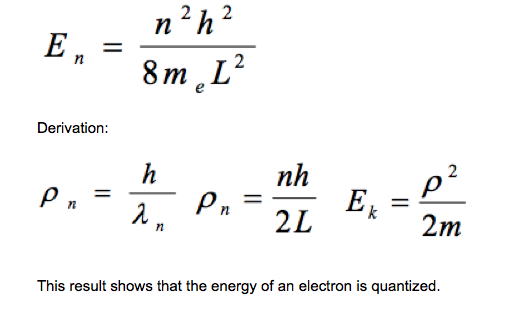The model assumes that, if an electron is confined to move in one dimension by a box, the de Broglie waves associated with the electron will be standing waves of wavelength 2L/n where L is the length of the box and n is a positive integer. Students should be able to show that the kinetic energy EK of the electron in the box is given by (see image):

The model assumes that electrons in the atom may be described by wavefunctions. The electron has an undefined position, but the square of
the amplitude of the wavefunction gives the probability of finding the electron at a particular point.
Electrons orbit in a probability region or electron cloud. The solution to the equation predicts exactly the line spectra of the hydrogen atom.

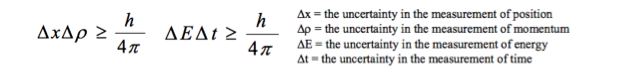Students should be aware that the conjugate quantities, position–momentum and time–energy, cannot be known precisely at the same time. They should know of the link between the uncertainty principle and the de Broglie hypothesis. For example, students should know that, if a particle has a uniquely defined de Broglie wavelength, then its momentum is known precisely but all knowledge of its position is lost.

One experiment that can be used is the Geiger Marsden experiment. An estimate of the radii of nuclei can come about through the principle of the conservation of energy. The KE of a particle approaching a nucleus is completely transformed into electrostatic potential energy. At the distance of closest approach, the KE will be converted entirely to PE. The particle will be momentarily at rest.Use of energy conservation for determining closest-approach distances for Coulomb scattering experiments is sufficient.

Students should be able to draw a schematic diagram of the Bainbridge mass spectrometer, but the experimental details are not required. Students should appreciate that nuclear mass values provide evidence for the existence of isotopes. Positive ions of elements are pass through / accelerated through electric and magnetic fields. Particles will pass into a detector. The mass of the nuclei can then be determined. eE = Bev or v = E/B

For example, alpha (α) particles produced by the decay of a nucleus have discrete energies; gamma-ray (γ-ray) spectra are discrete. Students should appreciate that the nucleus, like the atom, is a quantum system and, as such, has discrete energy levels. When a nucleus decays by emitting an alpha particle or a gamma ray, the particles or photons emitted are only at specific energies (there is not a complete range of energies emitted, only certain specific levels). An alpha particle or photon thus has an energy equal to the difference between energy levels of the nucleus. The gamma and alpha particle energies are characteristic of the emitting nucleus. The existence of nuclear energy levels is proven.

Students should know that β energy spectra are continuous, and that the neutrino was postulated to account for these spectra.

Students should know that the decay constant is defined as the probability of decay of a nucleus per unit time. If the number of nuclei present in a sample at t = 0 is N₀, the number N still present at time t later is given by N = N_oe^-λt where λ is the decay constant (the probability that a nucleus will decay in unit time).