Cards In This Set
| Front | Back |
|
1.1.1: State and compare quantities to the
nearest order of magnitude.
|
If quantity > 3.16, round to next order of magnitude.
|
|
1.1.2: State the ranges of magnitude of
distances, masses and times that
occur in the universe, from smallest to
greatest.
|
Distances: from 10–15 m to 10+25 m (sub-nuclear
particles to extent of the visible universe).
Masses: from 10–30 kg to 10+50 kg (electron to mass of
the universe).
Times: from 10–23 s to 10+18 s (passage of light across a
nucleus to the age of the universe).
|
|
1.1.3: State ratios of quantities as differences
of orders of magnitude.
|
For example, the ratio of the diameter of the
hydrogen atom to its nucleus is about 105, or a
difference of five orders of magnitude.
|
|
1.2.1: State the fundamental units in the SI
system.
|
 Students need to know the following: kilogram, meter, second, ampere, mole and kelvin. |
|
1.2.2: Distinguish between fundamental
and derived units and give examples
of derived units.
|
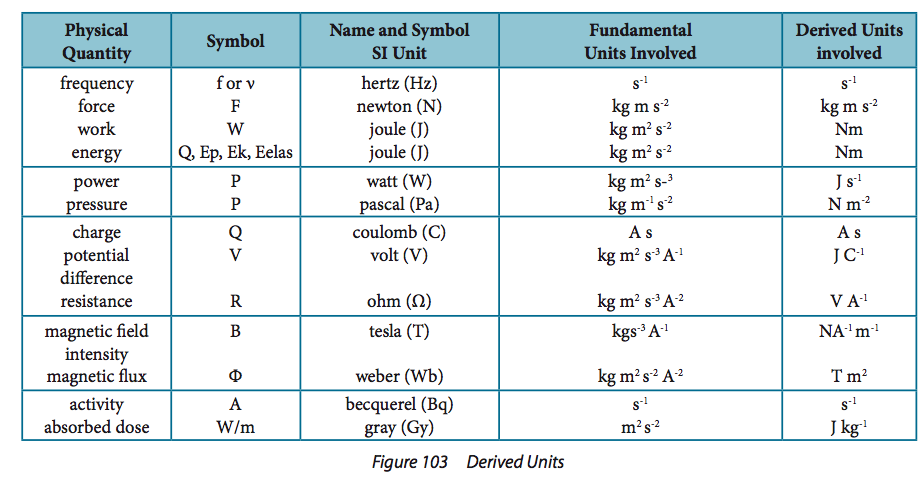 Fundamental Units – seven basic units of the SI measurement system: kilogram, second, mole, meter, ampere, Kelvin, candela. Derived Units – units that are combinations of fundamental units. These combinations may or may not have a separate name. (eg. 1 kg m/s2 = 1 N) |
|
1.2.3:
Convert between different units of
quantities.
|
For example, J and kW h, J and eV, year and second,
and between other systems and SI.
|
|
1.2.4: State units in the accepted SI format.
|
Students should use m s–2 not m/s2 and m s–1 not
m/s.
|
|
1.2.5:
State values in scientific notation and
in multiples of units with appropriate
prefixes.
|
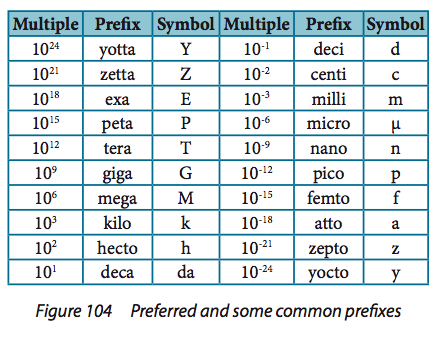 For example, use nanoseconds or gigajoules. |
|
1.2.6:
Describe and give examples of
random and systematic errors.
|
Random Uncertainty - An uncertainty produced by unknown and unpredictable
variations in the experimental situation, such as temperature fluctuations and
estimations when reading instruments. (Affects
the precision of results - Can be reduced by taking repeated trials but not
eliminated – shows up as error bars on a graph)
Systematic Error - An
error associated with a particular instrument or experimental technique that
causes the measured value to be off by the same amount each time. (Affects
the accuracy of results - Can be eliminated by fixing source of error – shows
up as non-zero y-intercept on a graph)
|
|
1.2.7:
Distinguish between precision and
accuracy.
|
Accuracy
- An
indication of how close a measurement is to the accepted value (a measure of correctness).
Precision - An indication of the agreement among a number of measurements made in the same way (a measure of exactness). |
|
1.2.8:
Explain how the effects of random
errors may be reduced.
|
Multiple trials.
Students should be aware that systematic errors are
not reduced by repeating readings.
|
|
1.3.1:
Distinguish between vector and scalar
quantities, and give examples of each.
|
A vector is represented in print by a bold italicized
symbol, for example, F.
Vector – a quantity with both a magnitude and a direction e.g. velocity Scalar – a quantity with magnitude only e.g. speed |
|
2.1.1:
Define displacement, velocity, speed
and acceleration.
|
1.
Displacement (s) - distance traveled from a
fixed point in a particular direction
2.
*Velocity (u,v) - rate of change of displacement
3.
*Speed (u,v) - rate
of change of distance
4.
*Acceleration (a) - rate
of change of velocity
|
|
2.1.2: Explain the difference between
instantaneous and average values of
speed, velocity and acceleration.
|
Instantaneous: one point in time, infinitesimally small
Average: Over a period of time |
|
2.1.3: Outline the conditions under
which the equations for uniformly accelerated motion may be applied. |
Acceleration is constant, not changing.
|



