Cards In This Set
| Front | Back |
|
When identifying the intervals for increasing, decreasing, and constant, which variables do we focus on?
|
The x's
because we are looking from left to right mark the changes on the x-axis |
|
When is a graph increasing? |
The picture is rising (as you move from left to right) |
|
When is a graph decreasing?
|
 The picture is "falling" (as you move from left to right) |
|
When is a graph constant?
|
 The picture doesn't change (as you move from left to rignt) |
|
What is the sentence for Relative Maximum/Minimum?
|
Relative (maximum/minimum) of (y-value) when x = (x value)
|
|
What is a relative maximum?
|
The highest point in a region. (a hill)
|
|
What is a relative minimum?
|
The lowest point in a region. (a valley)
|
 What is the equation for this graph? |
Y = x
|
 What is the equation for this graph? |
Y = x2
|
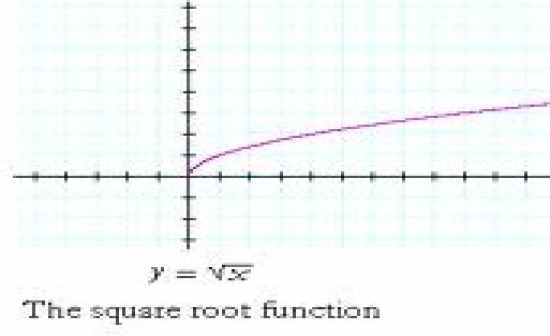 What is the equation for this graph? |
Y = /x (square root of x)
|
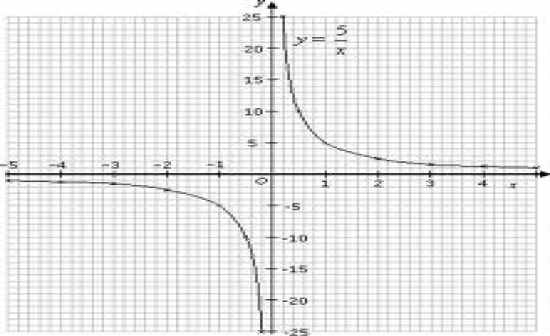 What is the equation for this graph? |
Y = 1/x
|
|
How do you find the solution for (f <> g) (#) when <> is addition, subtraction, multiplication, or division?
|
Find f(#)
Find g(#) Then perform the operation <> on the two answer |
|
How is the domain of f/g different from f+g, f-g, or fg?
|
The domain if f/g is the domain of the others minus all the numbers where g(x) = 0.
|
|
How do you evaluate (fog)(#)?
|
Find g(#).
Then plug the answer from above into f. The answer from the second step is the answer to the question. |



