Cards In This Set
| Front | Back |
|
Teorema: razionali.
|
Non esiste alcun numero razionale p/q tale che:
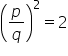 |
|
Definizione: numero reale.
|
Definiamo numero reale unallineamento decimale con segno,
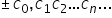 Se l'allineamento è periodicoil numero è razionale. Se l'allineamento non è periodico il numero è irrazionale. Se l'allineamento è periodicoil numero è razionale. Se l'allineamento non è periodico il numero è irrazionale. |
|
Teorema: proprietà dell'ordinamento su R.
|
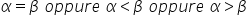 |
|
Teorema: di densità.
|
Tra due numeri reali esistono infiniti numeri razionali e infiniti numeri irrazionali
|
|
Definizione: massimo e minimo.
|
Un numero reale si dice massimo di un sottoinsieme
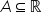 se se 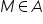 e e 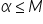 per ogni per ogni 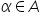 Un numero reale m si dice minimo di un sottoinsieme 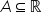 se se 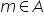 e e 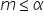 per ogni per ogni 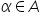 |
|
Teorema: di completezza.
|
Se A è un insieme limitato superiormente, l'insieme del maggioranti di A ha massimo. Se A è un insieme limitato inferiormente, l'insieme dei minoranti di A ha minimo.
|
|
Definizione: estremo superiore e inferiore.
|
Se A è limitato superiormente, definiamo estremo superiore di A il minimo dei maggioranti di A. Se A è limitato inferiormente, definiamo estremo inferiore di A il massimo dei maggioranti di A. Per l'estremo superiore e inferiore usiamo le notazioni supA, inf A.
|
|
Teorema: elemento separatore di R.
|
Siano A e B due insiemi non vuoti e separati di numeri reali tali che
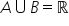 Allora esiste un unimo numero reale y tale: Allora esiste un unimo numero reale y tale: 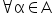 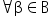 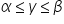 Inoltre, o y è il massimo di A, o y è il minimo di B. |
|
Teoerma: archimedeo.
|
Per ogni
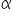 e e 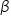 positivi esiste un intero n > 0 tale che n positivi esiste un intero n > 0 tale che n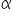 > >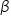 . . |
|
Lemma: disuguaglianza fondamentale.
|
Assegnati un intero
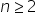 e un numero reale e un numero reale 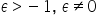 si ha si ha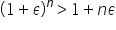 . . |
|
Teorema: radice n-esima.
|
Fissato un intero
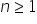 e un numero reale e un numero reale 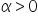 , esiste uno ed un solo reale , esiste uno ed un solo reale 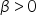 tale che tale che 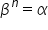 . . |
|
Definizione: radice n-esima.
|
Il numero
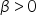 che soddisfa che soddisfa 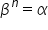 si chiama radice n-esima di si chiama radice n-esima di 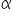 e si indica con il simbolo e si indica con il simbolo 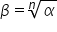 IL numero 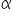 si chiama radicando e n si chiama indice della radice. Si usa anche la notazione si chiama radicando e n si chiama indice della radice. Si usa anche la notazione 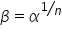 |
|
Definizione: potenze a esponente razionale.
|
SIa m è un intero relativo, sia
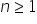 un intero e sia un intero e sia 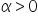 . Si pone . Si pone 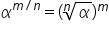 . . |
|
Definizione: potenze a esponente reale.
|
Sia
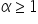 e e 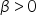 . Poniamo . Poniamo 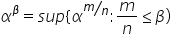 Se 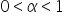 e e 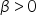 poniamo poniamo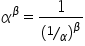 Se 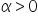 e e 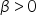 poniamo poniamo 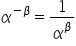 Infine poniamo 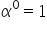 In tal modo la potenza In tal modo la potenza 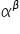 risulta definita per ogni risulta definita per ogni 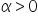 e e 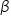 reale. reale. |
|
Teorema: logaritmo.
|
Sia
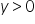 e e 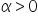 , , 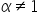 . Esiste uno e un solo numero reale x tale che . Esiste uno e un solo numero reale x tale che 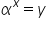 . . |





