Cards In This Set
| Front | Back |
|
C-1 Linear Pair
Conjecture
|
If two angles form
a linear pair, then the measures of the angles add up to
180°
|
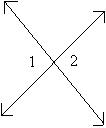 C-2 Vertical Angles Conjecture |
If two angles are vertical angles, then they are congruent (have equal
measures)
|
|
C-3a Corresponding Angles Conjecture (CA)
|
If two parallel lines are cut by a transversal, then
corresponding angles are congruent
|
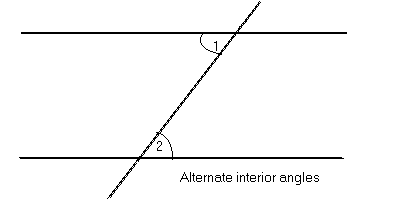 C-3b Alternate Interior Angles Conjecture (AIA) |
If two parallel
lines are cut by a transversal, then
alternate interior angles are congruent
|
 C-3c Alternate Exterior Angles Conjecture (AEA) |
If two parallel lines are cut by a transversal, then
alternate exterior angles are congruent
|
|
C-3 Parallel Lines Conjecture
|
If two parallel lines are cut by a transversal, then corresponding angles are
congruent, alternate interior angles are congruent, and alternate exterior angles are congruent
|
|
C-4 Converse of the Parallel Lines Conjecture
|
If two lines are cut by a transversal to form pairs of
congruent corresponding angles, congruent alternate interior angles, or congruent alternate exterior
angles, then the lines are parallel
|
|
C-5 Perpendicular Bisector Conjecture
|
If a point is on the perpendicular bisector of a segment, then it is equidistant from the endpoints
|
|
C-6 Converse of the
Perpendicular Bisector Conjecture
|
If a point is equidistant from the endpoints of a
segment, then it is on the perpendicular bisector of the segment
|
|
C-7 Shortest Distance Conjecture
|
The shortest distance from a point to a line is measured along the perpendicular segment from the point to the line
|
|
C-8 Angle Bisector
Conjecture
|
If a point is on the bisector of an angle, then it is equidistant from the sides of the angle
|
|
C-9 Angle Bisector
Concurrency Conjecture
|
The three angle bisectors of a triangle are concurrent (meet at a point)
|
|
C-10 Perpendicular
Bisector Concurrency Conjecture
|
The three perpendicular bisectors of a triangle are concurrent
|
|
C-11 Altitude Concurrency Conjecture
|
The three altitudes (or the lines containing the altitudes) of a triangle are concurrent
|
|
C-12 Circumcenter Conjecture
|
The circumcenter of a triangle is equidistant from the vertices
|



